Simple Graph Coloring Algorithm

Two players Alice and Bob alternately color the vertices of G using colors from a set of colors X with Xr. A graph is k-colorableif there is a proper k-coloring.

Simple Graph Coloring Algorithm - If you're looking for video and picture information related to the key word you have come to visit the ideal site. Our site provides you with suggestions for seeing the highest quality video and image content, hunt and locate more informative video content and images that fit your interests. includes one of thousands of movie collections from several sources, especially Youtube, therefore we recommend this video that you see. This site is for them to visit this site.

Graph Coloring Problem Techie Delight

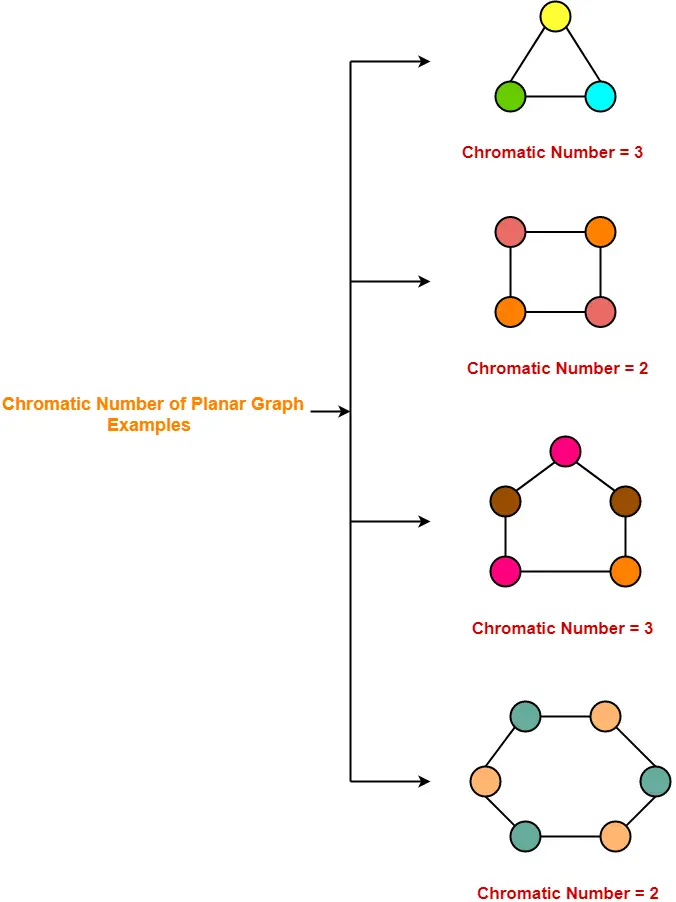
Most often we use C k Vertices of the same color form a color class.

Simple graph coloring algorithm. The idea of coloring a graph is very straightforward and it seems as if it should be. Put the vertex back. It is an assignment of labels traditionally called colors to elements of a graph subject to certain constraintsIn its simplest form it is a way of coloring the vertices of a graph such that no two adjacent vertices share the same color.

15 minutes Coding time. 1 Basic deﬁnitions and simple properties A k-coloringof a graph G VE is a function c. Graph coloring is nothing but a simple way of labelling graph components such as vertices edges and regions under some constraints.

Coloring the graph Now that we have method findColorForVertex the simple algorithm to color the graph is given to the right. Color the rest of the graph with a recursive call to Kempes algorithm. Thechromatic number χG of a.

Time and space analayis Assume the graph is given as an adjacency list in some form and that it takes constant time to get the outdegree of a vertex. 5 Bipartite Graphs. A color αX is a legal color for uncolored vertex v if by coloring v with color α the subgraph induced by all vertices of color α has maximum degree at most d.

There is an M P C algorithm that in O log Δ log log n O log log n rounds whp. Every planar graph has at least one vertex of degree 5. Color first vertex with first color.

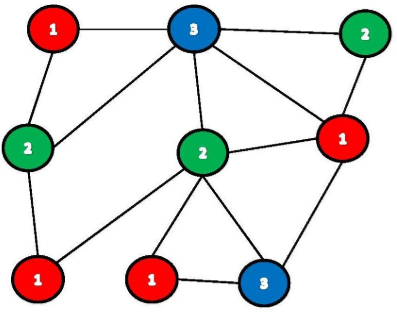
It ensures that no two adjacent vertices of the graph are colored with the same color. In a graph no two adjacent vertices adjacent edges or adjacent regions are colored with minimum number of colors. Graph Coloring is a process of assigning colors to the vertices of a graph.

Try For Free Today. Ad Tableau Helps People Transform Data Into Actionable Insights. The present section introduces the simple decentralized graph coloring SDGC algorithm.

Connect Your Data to Tableau for Actionable Insights. V C where C k. Given a number of colors k SDGC is based on iteratively improving an initial random assignment of colors to the vertices of the graph.

In graph theory graph coloring is a special case of graph labeling. A simple program to visualize greedy graph coloring algorithm Only requires pygame 20. Geographical maps of countries or states where no two adjacent cities cannot be assigned same color.

A simple algorithm for graph coloring is easy to describe but potentially extremely expensive to run. Connect Your Data to Tableau for Actionable Insights. Basic Greedy Coloring Algorithm.

This is called a vertex coloring. Try For Free Today. If a given graph is 2-colorable then it is Bipartite otherwise not.

It is adjacent to at most 5 vertices which use up at most 5 colors from your palette. Kempes graph-coloring algorithm To 6-color a planar graph. At each turn procedure 31 takes at most nm 5 steps by proposition 41.

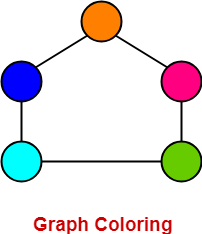
A coloring is proper if adjacent vertices have different colors. Kierstead Department of Mathematics Arizona State University Main Campus PO. Download the Free Trial Today.

The controls are a bit weird but anyway. Each player is required to color legally on each turn. Perhaps more importantly we bound the game coloring number of a graph G in terms of a new parameter rG.

This is a slight improvement of the current. Four colors are sufficient to color any map See Four Color Theorem. We can check if a graph is Bipartite or not by coloring the graph using two colors.

The global goal of SDGC is to minimize the number of conflicts in the graph that is the number of edges connecting two vertices with the same color. We use this result to give very easy proofs of the best known upper bounds on game coloring number for forests interval graphs chordal graphs outerplanar graphs and line graphs. Down Generate a random graph Up Decrease the max number of nodes Right Increase max number of nodes Left Color nodes sequentially.

Given a simple graph Gwith nvertices and mcolors part I of the algorithm takes at most nm 7 nm 6 nm 4 nm 2 steps. Chromatic Number is the minimum number of colors required to properly color any graph. The basic algorithm never uses more than d1 colors where d is the maximum degree of a vertex in the given graph.

Box 871804 Tempe Arizona 85287-1804 Received January 13 1999 We prove that the game coloring number and therefore the game chromatic number of a planar graph is at most 18. We prove that the game coloring number and therefore the game chromatic number of a planar graph is at most 18. It doesnt guarantee to use minimum colors but it guarantees an upper bound on the number of colors.

A Simple Competitive Graph Coloring Algorithm H. Download the Free Trial Today. This number is called the chromatic number and the graph is called a properly colored graph.

See this for more details. Computes a Δ 1 list-coloring of an n-vertex graph with m edges and maximum degree Δ and that uses O n α memory per machine for an arbitrary constant α. Following is the basic Greedy Algorithm to assign colors.

Ad Tableau Helps People Transform Data Into Actionable Insights. This is a slight improvement of the current upper bound of 19.